Выборки элементов без повторений

Рассмотрим сначала некоторые общие термины.

• Пусть некоторая совокупность содержит n элементов, из которых выбирают k элементов. Каждый такой набор будем называть выборкой объема k из n элементов.
• Будем различать выборки с возвращением и без возвращения. Пусть имеется совокупность n пронумерованных элементов:
  • если отобранный элемент после выбора не возвращается в исходную совокупность и не может повторяться в данной выборке больше одного раза, то такая выборка называется выборкой без возвращения или без повторения;
  • если отобранный элемент после фиксации номера снова возвращается в исходную совокупность и, таким образом, может вновь оказаться в данной выборке, то говорят о выборке с возвращением или с повторением.
• Выборка называется упорядоченной, если порядок следования элементов в ней задан. Если две упорядоченные выборки отличаются только порядком следования элементов, то они считаются разными (например: 12 и 21).
• Выборка называется неупорядоченной, если порядок элементов в ней не имеет значения (т. е. 12 и 21 неразличимы).

Размещения без повторений.

Размещениями без повторений называются упорядоченные выборки, содержащие k различных элементов из данных n элементов.

Обратим внимание на следующие важные положения:

1. Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.
2. Порядок элементов в выборке важен.

Формула для определения числа размещений без повторений:

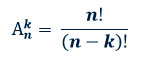
Задача. Дана последовательность символов А, Б, С. Сколько вариантов кода, состоящего из двух разных символов, можно составить из заданной последовательности?

Решение.По условию код состоит «из двух разных символов», при этом коды АБ и БА – не одинаковые, поэтому, выборки – размещения без повторений.
Выборка осуществляется из 3 элементов по 2. Значит, n = 3, k = 2.

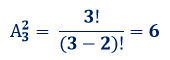
Действительно, комбинаций, удовлетворяющих условию, всего шесть: {АБ, АС, БА, БС, СА, СБ}

Перестановки без повторений.

Нетрудно заметить, что размещения, в которые входят все n разных элементов заданного множества (т. е. k = n), будут отличаться только порядком следования входящих элементов. Такие размещения называют перестановками.

Перестановками без повторений называются всевозможные упорядоченные выборки, составленные из всех данных n элементов.

Формула для определения числа перестановок без повторений
P_n = n! = n * (n − 1) * (n − 2) *...* 2 * 1

Задача. Сколько вариантов кода длиной 3 символа можно составить из трех букв А, Б, С, если каждая буква входит в последовательность не более одного раза?

Решение. Так как «каждая буква входит в последовательность не более одного раза», то выборки – перестановки без повторений.
P_n = 3! = 3 * 2 * 1 = 6 {АБC, АCБ, БАС, БСА, САБ, СБА}

Сочетания без повторений.

Сочетаниями без повторений называются неупорядоченные выборки, содержащие k различных элементов из данных n элементов.

Отметим, что

1. …«выборки неупорядоченные», т.е. выборки AB и ВА – это одно и тоже сочетание.
2. Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.

Формула для определения числа сочетаний без повторений:

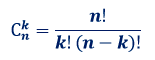
Задача. Из 4-х кандидатов происходят выборы участников конференции. Сколько существует вариантов выбора делегации?

Решение. Очевидно, один и тот же кандидат в данную выборку может быть избран только один раз. При этом набор А, Б и Б, А – это одни те же участники. Поэтому выборки есть сочетания без повторений.

Воспользуемся формулой для расчета числа различных сочетаний без повторений: