Алфавитный подход к измерению информации

Выдающийся советский математик прошлого века Андрей Николаевич Колмогоров предложил подход к измерению информации, который получил название алфавитный.

Согласно ему количество информации, содержащейся в последовательности символов, – это минимальное количество двоичных знаков, например, «0» и «1», необходимых для кодирования этой последовательности символов без учета содержания этого сообщения.

Определение. При алфавитном подходе один бит – это количество информации, которое можно передать сообщением из одного двоичного значка, то есть «0» или «1».

Важные особенности алфавитного подхода:

• сообщения, записанные на естественном языке, кодируются без учета их смыслового содержания (такой подход является объективным);
• каждый символ несёт одинаковое количество информации, не учитывается, что некоторые символы могут встречаться в сообщении чаще других.

Вернемся к эксперименту с бросанием монеты. Результат падения («орел», или «решка») можно закодировать двумя символами, например, 0 и 1. Тогда информация, которую несет нам один бросок, – это один бит. 5 бросков монетки можно закодировать пятью символами «0» и «1» – 5 бит информации. Таким образом, получившиеся результаты не противоречат результатам, полученным при содержательном подходе.

Значит, в случае равновероятного появления в любой позиции текста символов используемого алфавита, количество информации, которое несет один символ алфавита, можно вычислить по формуле Хартли.

Однако, в текстах, записанных на естественных языках, частота появление символов используемого алфавита различна (смотрите таблицу)

Частотные характеристики русских букв (кириллицы) в текстах

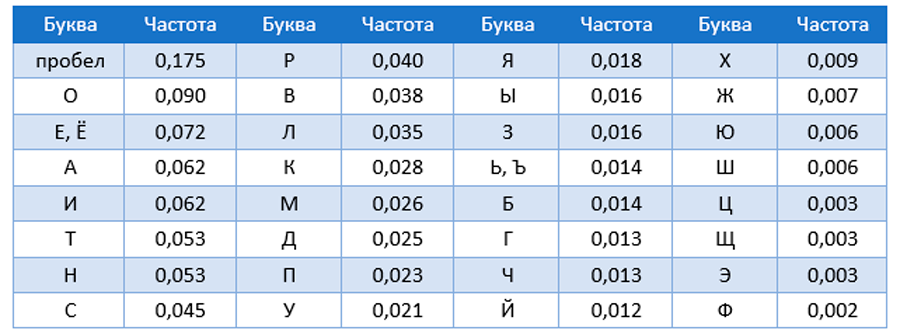
Для оценки среднего информационного веса символа с учетом разной вероятности их встречаемости используется формула Шеннона:

I = p₁ * log₂ (1 / p₁) + p₂ * log₂ (1 / p₂) + ... + p_N * log₂ (1 / p_N)
где p_i – вероятность появления i – го символа
N – количество символов, в алфавите

Формула Шеннона показывает средний информационный вес символа алфавита.