Кодирование информации
Для протекания процессов передачи, обработки и хранения информации необходимо ее зафиксировать с помощью определенной знаковой системы (алфавита), т. е. закодировать.
Кодирование – это процесс представления информации в виде последовательности условных обозначений.
Кодирование информации всегда происходит по определенным правилам. Правило кодирования называется кодом.
Последовательность символов известной длины из конечного набора знаков (алфавита) используемых для кодирования, называется кодовым словом (например, кодовое слово для буквы «O» в азбуке Морзе имеет длину равную трем и представляет последовательность из трех символов тире «— — —»).
Способы кодирования информации зависят от конкретной задачи. Так для передачи сообщений по радио и телеграфу долгое время применялась азбука Морзе, в которой для кодирования сообщений использовались последовательности электрических сигналов двух видов – короткого и длинного.
Создатель азбуки, американский художник и изобретатель Самюэль Морзе, в основу кодирования положил частоту встречаемости символов в тексте. В результате, код, состоящий из точек и тире, у разных букв мог иметь неодинаковую длину – от одного до шести символов. Из-за неравномерности кода различных букв для однозначного декодирования сообщения пришлось использовать третий символ – паузу, разделитель между буквами.
Кодовая таблица азбуки Морзе
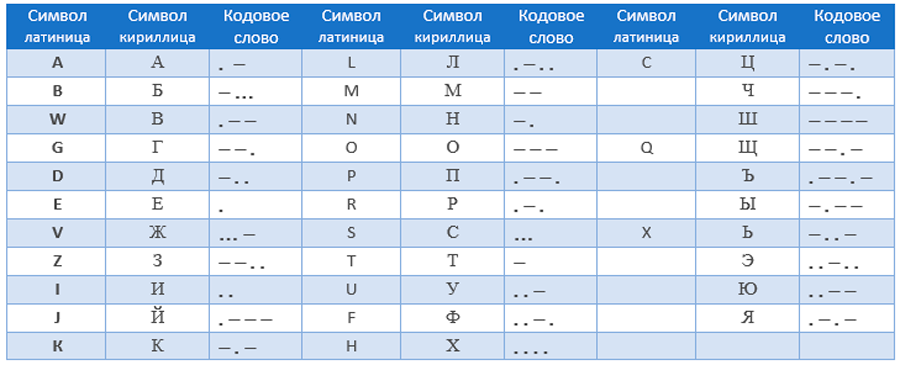
В 1870 году Жан Бодо изобрел равномерный телеграфный код, в котором использовалось всего два вида электрических сигналов. Длина кодов символов алфавита таблицы Бодо была одинаковой и равной пяти. Равномерный код позволил отказаться от разделителя между буквами и создал условия для автоматизации процесса передачи и печати букв.
Длина кодового слова в случае равномерного кода определяется количеством вариантов, которые необходимо закодировать. Рассмотрим задачу:
В забеге участвуют 125 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем в байтах сообщения, записанного устройством, после того как промежуточный финиш прошли 64 легкоатлета?
Решение.
- Заметим, что для представления номеров используется равномерный двоичный код (1 бит может хранить два состояния).
- Определим длину кодового слова. Очевидно, кодовые слова будут представлять собой упорядоченные выборки длиной k из двух символов. При этом символы в кодовом слове могут повторяться. Значит, эта выборка размещения с повторениями. Тогда
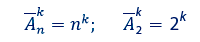
- Заданное количество необходимых номеров не равно степени числа 2, поэтому выбираем длину кодового слова с запасом:
125 ≤ 2 k
Таким образом, длина кодового слова равна 7 битам. - Определим информационный объем сообщения после того как промежуточный финиш прошли 64 легкоатлета:
64 • 7 бит = 448 бит = 56 байт
Ответ. 56 байт



